Question

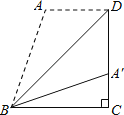
【题目】如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A′处，若∠A′BC＝20°，则∠A′BD的度数为_____°．

Answer 1

【答案】25．

【解析】

由折叠的性质可得：∠ABD=∠A′BD，∠A=∠BA′D，又由DC⊥BC，∠A′BC=20°，可求得∠A的度数，然后由AD∥BC，根据两直线平行，同旁内角互补，即可得∠A+∠ABD+∠A′BD+∠A′BC=180°，则可求得∠A′BD的度数．

根据折叠的性质可得：∠ABD＝∠A′BD，∠A＝∠BA′D，

∵DC⊥BC，

∴∠C＝90°，

∵∠A′BC＝20°，

∴∠BA′D＝∠A′BC+∠C＝110°，

∴∠A＝110°，

∵AD∥BC，

∴∠A+∠ABC＝180°，

即∠A+∠ABD+∠A′BD+∠A′BC＝180°，

∴110°+2∠A′BD+20°＝180°，

∴∠A′BD＝25°．

故答案为：25．