题目内容
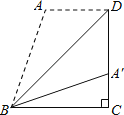
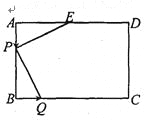
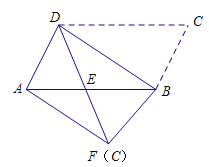
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据折叠的性质可证∠CDB =∠EDB,由平行四边形的性质,可证∠CDB =∠EBD,等量代换可证得结论;
(2)根据(1)结论可知DE=BE,然后由平行四边形的对边相等和等量代换,可知AE=EF,从而根据等边对等角可得∠EAF=∠EFA,再由三角形的内角和得出∠EDB= ∠EFA,因此可证得AF∥BD(或由AB与BD互相平分证得四边形ADBF是平行四边形).
(1)由折叠可知:∠CDB =∠EDB
∵四边形ABCD是平行四边形
∴DC∥AB
∴∠CDB =∠EBD
∴∠EDB=∠EBD
(2)∵∠EDB=∠EBD
∴DE=BE
由折叠可知:DC=DF
∵四边形ABCD是平行四边形
∴DC=AB
∴AE=EF
∴∠EAF=∠EFA
△BED中,∠EDB+∠EBD+∠DEB=180°
即2∠EDB+∠DEB=180°
同理△AEF中,2∠EFA+∠AEF=180°
∵∠DEB=∠AEF
∴∠EDB= ∠EFA
∴AF∥BD

【题目】实验中学附近某水果超市最近新进了一批火龙果,每斤8元,为了合理定价,在第一周试行机动价格,卖出时每斤以10元为标准,超出10元的部分记为正,不足10元的部分记为负,超市记录第一周火龙果的售价情况和售出情况:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每斤相对于标准价格(元) | +1 | -2 | +3 | -1 | +2 | +5 | -4 |
售出斤数 | 20 | 35 | 10 | 30 | 15 | 5 | 50 |
(1)这一周超市售出的火龙果单价最高的是星期 , 最高单价是 元.
(2)这一周超市总共售出火龙果多少斤?总共卖得多少元钱?
(3)这一周超市出售此种火龙果的收益如何?(盈利或亏损的钱数)