题目内容
【题目】下列结论:①平面内3条直线两两相交，共有3个交点;②在平面内，若∠AOB =40°，∠AOC= ∠BOC,则∠AOC的度数为20°;③若线段AB=3, BC=2，则线段AC的长为1或5;④若∠a+∠β=180°，且∠a<∠β，则∠a的余角为
(∠β-∠a).其中正确结论的个数（ ）
A.1个B.2个C.3个D.4个
【答案】A
【解析】
根据相交线的定义，角平分线的定义，线段的和差，余角和补角的定义进行判断找到正确的答案即可.
解：①平面内3条直线两两相交，如下图，
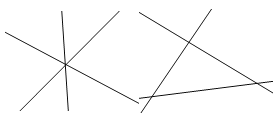
有1个（左图）或3个交点（右图），故错误；
②在平面内，若∠AOB=40°，∠AOC=∠BOC，如下图，
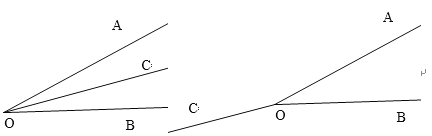
∠AOC的度数为20°（左图）或160°（右图），故错误；
③若线段AB=3，BC=2，因为点C不一定在直线AB上，所以无法求得AC的长度，故错误；
④若∠α+∠β=180°，则
，则当∠a<∠β时，
，则
，故该结论正确.
故正确的有一个，选：A．
【题目】参照学习函数的过程与方法，探完函数y＝
（x≠0）的图象与性质，因为y＝＝1﹣
，即y＝﹣+1，所以我们对比函数y＝﹣来探究．
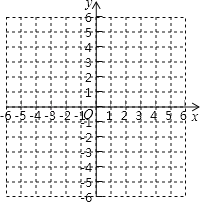
操作：面出函数y＝（x≠0）的图象．
列表：
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y＝﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
y＝ | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点：在平面直角坐标中，以自变量x的取值为横坐标，以y＝相应的函数值为纵坐标，描出如图所示相应的点；
连线：请把y轴左边和右边各点，分别用一条光滑曲线顺次连接起来．
观察：由图象可知：
①当x＞0时，y随x的增大而 （填“增大”或“减小”）
②y＝的图象可以由y＝﹣的图象向 平移 个单位长度得到．
③y的取值范围是 ．
探究：①A（m1，n1），B（m2，n2）在函数y＝图象上，且n1+n2＝2，求m1+m2的值；
②若直线l对应的函数关系式为y1＝kx+b，且经过点（﹣1，3）和点（1，﹣1），y2＝，若y1＞y2，则x的取值范围为 ．
延伸：函数y＝
的图象可以由反比例函数y＝ 的图象向 平移 个单位，再向 平移 个单位得到．
