题目内容
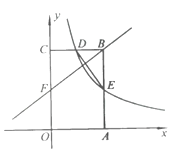
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
【答案】(1)k=3,(2,![]() )(2)y=
)(2)y=![]()
【解析】
分析: (1)先根据点B的坐标为(2,3)求出D点坐标,代入反比例函数解析式即可求出k的值,进而得出解析式,再把x=2代入求出y的值即可得出E点坐标,
(2)根据FB⊥DE,利用同角的余角相等得到一组等角,再根据两直角相等进而得出△FBC∽△DEB,根据相似三角形的性质进而求出F点的坐标,利用待定系数法求出直线FB的解析式即可.
详解:(1)∵点B的坐标为(2,3),点D是BC的中点,
∴D(1,3),
∵点D在反比例函数![]() (x>0)上,
(x>0)上,
∴3=![]() ,解得k=3,
,解得k=3,
∴反比例函数的解析式为:![]() .
.
∵四边形OABC是矩形,点B的坐标为(2,3),
∴当x=2时,y=![]() ,
,
∴E点坐标为(2,![]() )
)
(2)因为FB⊥DE,
∴∠CBF+∠EDB=90°,∠BED+∠EDB=90°,
∴∠CBF=∠BDE,
因为∠C=∠DBE=90°,
∴△FBC∽△DEB,
∵点E的坐标为(2,![]() ),B的坐标为(2,3),点D的坐标为(1,3),
),B的坐标为(2,3),点D的坐标为(1,3),
∴BD=1,BE=![]() ,BC=2,
,BC=2,
∵△FBC∽△DEB,
∴![]() ,
,
即:![]() ,
,
∴FC=![]() ,
,
∴点F的坐标为(0,![]() ),
),
设直线FB的解析式y=kx+b,
则2k+b=3,b=![]() ,
,
解得:k=![]() ,
,
∴直线FB的解析式y=![]() .
.
点睛:本题主考查反比例函数与几何综合,解决本题的关键是要熟练掌握反比例函数图象上点的坐标特征,要求学生利用相似三角形的性质进行综合分析.

练习册系列答案
相关题目