题目内容
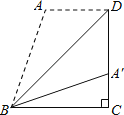
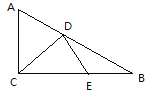
【题目】在Rt△ABC中，∠ACB=90°，AC=4，BC=8，D，E是AB和BC上的动点，连接CD，DE则CD+DE的最小值为（ ）
A. 8 B. 
C. 
D. 
【答案】D
【解析】
根据轴对称的性质，可得C的对称点C’，然后过C’作垂线可得C’E，再根据垂线段最短可知CD+DE最短，再利用直角三角形的性质求得CC’的长，继而得知△CC’E∽△ABC，利用相似三角形的对应边成比例，求出答案.
过C作C关于AB的对称点C’，然后过C’作C’E⊥BC，垂足为E，交AB于D，则C’E=C’D+DE=CD+DE最短，
∵AC=4,BC=8
∴AB=
∴CF=
=
即CC’=
∵∠C’+∠C’CB=∠B+∠C’CB=90°
∴∠C’=∠B
∴△C’CE∽△ABC
∴
∴C’E=
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
【题目】实验中学附近某水果超市最近新进了一批火龙果，每斤8元，为了合理定价，在第一周试行机动价格，卖出时每斤以10元为标准，超出10元的部分记为正，不足10元的部分记为负，超市记录第一周火龙果的售价情况和售出情况:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每斤相对于标准价格（元） | +1 | -2 | +3 | -1 | +2 | +5 | -4 |
售出斤数 | 20 | 35 | 10 | 30 | 15 | 5 | 50 |
（1）这一周超市售出的火龙果单价最高的是星期 ， 最高单价是 元．
（2）这一周超市总共售出火龙果多少斤？总共卖得多少元钱？
（3）这一周超市出售此种火龙果的收益如何？(盈利或亏损的钱数)
