��Ŀ����
����Ŀ����ͼ���ھ���![]() �У���
�У���![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ����
����![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ���ϣ�ֱ��
���ϣ�ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .��������ƽ���ڵ�ֱ�ߣ��Ƚ���ֱ������ƽ��
.��������ƽ���ڵ�ֱ�ߣ��Ƚ���ֱ������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ�����ֱ���˶���Ϊֱ�ߵ�бƽ��.�ֽ�ֱ��
����λ���ȣ�����ֱ���˶���Ϊֱ�ߵ�бƽ��.�ֽ�ֱ��![]() ����
����![]() ��бƽ�ƣ��õ�ֱ��
��бƽ�ƣ��õ�ֱ��![]() .
.


������ͼ��
��1����ֱ��![]() ����������Χ�ɵ������
����������Χ�ɵ������
��2����ֱ��![]() ��
��![]() �Ľ������ꣻ
�Ľ������ꣻ
��3���ڵ�һ�����ڣ���ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �ǵ���ֱ�������Σ������ڣ���ֱ��д����
�ǵ���ֱ�������Σ������ڣ���ֱ��д����![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
���𰸡���1��![]() ����2��ֱ��
����2��ֱ��![]() ��
��![]() �Ľ�������
�Ľ�������![]() ����3�����ڵ�
����3�����ڵ�![]() �����꣺
�����꣺![]() ��
��![]() ��
��![]() .
.
��������
1��ֱ��![]() ����������Χ�ɵ����
����������Χ�ɵ����![]() ��������⣻
��������⣻
��2����ֱ��![]() ����2��бƽ�ƣ��õ�ֱ��
����2��бƽ�ƣ��õ�ֱ��![]() ��������⣻
��������⣻
��3����![]() Ϊֱ�ǡ�
Ϊֱ�ǡ�![]() Ϊֱ�ǡ�
Ϊֱ�ǡ�![]() Ϊֱ������������ɵ���ֱ�������ι���K����ȫ�ȣ������꽨�����̷ֱ���⼴�ɣ�
Ϊֱ������������ɵ���ֱ�������ι���K����ȫ�ȣ������꽨�����̷ֱ���⼴�ɣ�
�⣺��1��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
![]() ֱ��
ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
![]() ��
��![]() ����
����![]() ����
����
![]() �����
�����![]() ��
��
![]() ֱ��
ֱ��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
��2��![]() ��ֱ��
��ֱ��![]() ����
����![]() ��бƽ�ƣ��õ�ֱ��
��бƽ�ƣ��õ�ֱ��![]()
![]() ֱ��
ֱ��![]()
![]() ֱ��
ֱ��![]()
��![]() ��
��![]()
��ֱ��![]() ��
��![]() �Ľ�������
�Ľ�������![]() ��
��
��3���ٵ�![]() Ϊֱ��ʱ����ͼ1��ʾ���ڵ�һ�����ڣ���ֱ��
Ϊֱ��ʱ����ͼ1��ʾ���ڵ�һ�����ڣ���ֱ��![]() �ϲ����ڵ�
�ϲ����ڵ�![]() ��
��
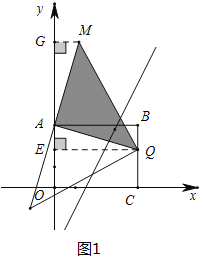
�ڵ�![]() Ϊֱ��ʱ��
Ϊֱ��ʱ��![]() ��
��
����![]() ��
��![]() ���ƽ���߷ֱ�
���ƽ���߷ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����ͼ��3��
����ͼ��3��
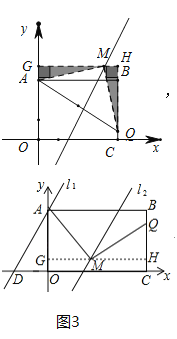 ��
��
���![]() ����
����![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ������
������![]() ��
��
��ã�![]() ��
��![]() ��
��
�ʵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�۵�![]() Ϊֱ��ʱ����ͼ4��ʾ��
Ϊֱ��ʱ����ͼ4��ʾ��
 ��
��
��Q����FQ��ֱ��y�ᴹ��ΪF����M����MG��ֱFQ����ΪG��
ͬ���ɵã�FQ=MG��AF=DG��
��Q��������4��n����0��n��3����AF=DG=3-n��FQ=MG=4
��M��������7-n��4+n����
����![]() ����
����![]() ��
��
��ã�![]()
�ʵ�![]() ��
��
������������![]() �����꣺
�����꣺![]() ��
��![]() ��
��![]()