题目内容
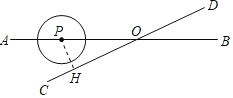
【题目】如图，直线AB、CD相交于点O，∠AOC=30°，半径为2cm的P的圆心在射线OA上，且与点O的距离为6cm，如果P以1cm/s的速度沿直线AB由A向B的方向移动，那么P与直线CD相切时☉P运动的时间是（ ）
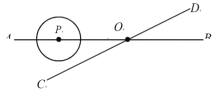
A.3秒或10秒B.3秒或8秒C.2秒或8秒D.2秒或10秒
【答案】D
【解析】
作PH⊥CD于H，根据直角三角形的性质得到OP＝2PH，分点P在OA上、点P在AO的延长线上两种情况可，根据切线的性质解答．
解：作PH⊥CD于H，
在Rt△OPH中，∠AOC＝30°，
∴OP＝2PH，
当点P在OA上，⊙P与直线CD相切时，OP＝2PH＝4cm，
∴点P运动的距离为6﹣4＝2，
∴⊙P运动的时间是2秒，
当点P在AO的延长线上，⊙P与直线CD相切时，OP＝2PH＝4cm，
∴点P运动的距离为6+4＝10，
∴⊙P运动的时间是10秒，
故选：D．
练习册系列答案
相关题目
