题目内容
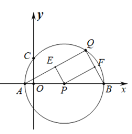
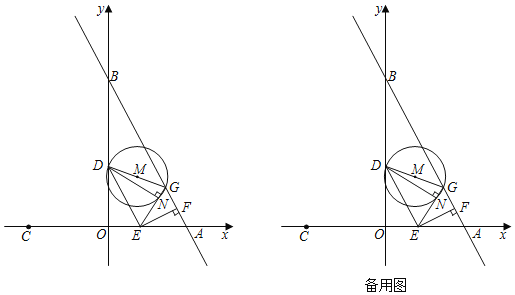
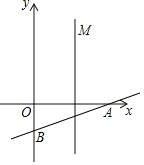
【题目】如图，直线y＝
x﹣2与x轴、y轴分别交于点A、B，过点C（2，﹣1）作直线l∥y轴，点M为直线l上的一个动点，以点M为圆心，MO为半径作圆，当⊙M与直线AB相切时，点M的坐标为_____．
【答案】（2，4）．
【解析】
由题意可得点C在AB上，通过证明△BCD∽△MCE，可得
，即可求点M坐标．
解：设点M（2，a）
∵当x＝2时，y＝
×2﹣2＝﹣1
∴点C在AB上，
∵⊙M与直线AB相切于点E
∴ME⊥AB
如图，过点B作BD⊥MC于点D，
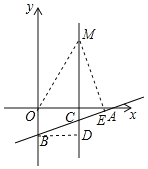
∵直线y＝x﹣2与x轴、y轴分别交于点A、B，
∴点B（0，﹣2）
∴BD＝2，CD＝1
∴BC＝
＝
∵点M（2，a），点O（0，0），点C（2，﹣1）
∴MO＝
＝ME，MC＝a+1
∵∠BCD＝∠MCE，∠MEC＝∠BDC＝90°
∴△BCD∽△MCE
∴
即
∴a＝4
∴点M（2，4）
故答案为：（2，4）
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
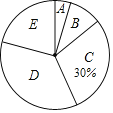
【题目】某校九年级学生参加了中考体育考试．为了了解该校九年级（1）班同学的中考体育成绩情况，对全班学生的中考体育成绩进行了统计，并绘制出以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：
分组 | 分数段（分） | 频数 |
A | 36≤x＜41 | 2 |
B | 41≤x＜46 | 5 |
C | 46≤x＜51 | 15 |
D | 51≤x＜56 | m |
E | 56≤x＜61 | 10 |
（1）m的值为 ；
（2）该班学生中考体育成绩的中位数落在 组；（在A、B、C、D、E中选出正确答案填在横线上）
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
