题目内容
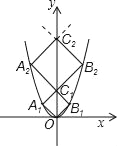
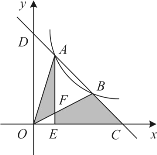
【题目】如图,一次函数 y=-x+b 与反比例函数y=![]() (x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
(x>0)的图象交于 A,B 两点,与 x 轴、y轴分别交于C,D 两点,连接 OA,OB,过 A 作 AE⊥x 轴于点 E,交 OB 于点F,设点 A 的横坐标为 m. 若 S△OAF+S 四边形 EFBC=4,则 m 的值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
作AM⊥OD于M,BN⊥OC于N.记△AOF面积为S,则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),所以S△ADM=2S△OEF,推出EF=![]() AM=
AM=![]() NB,得B(2m,
NB,得B(2m,![]() )代入直线解析式即可解决问题.
)代入直线解析式即可解决问题.
作AM⊥OD于M,BN⊥OC于N.

∵反比例函数y=![]() ,一次函数y=-x+b都是关于直线y=x对称,
,一次函数y=-x+b都是关于直线y=x对称,
∴AD=BC,OD=OC,DM=AM=BN=CN,记△AOF面积为S,
则△OEF面积为2-S,四边形EFBC面积为4-S,△OBC和△OAD面积都是6-2S,△ADM面积为4-2S=2(2-s),
∴S△ADM=2S△OEF,
由对称性可知AD=BC,OD=OC,∠ODC=∠OCD=45°,△AOM≌△BON,AM=NB=DM=NC,
∴EF=![]() AM=
AM=![]() NB,
NB,
∴EF是△OBN的中位线,
∴N(2m,0),
∴点B坐标(2m,![]() )代入直线y=-x+m+
)代入直线y=-x+m+![]() ,
,
∴![]() =-2m+m+
=-2m+m+![]() ,整理得到m2=2,
,整理得到m2=2,
∵m>0,
∴m=![]() .
.
故答案为![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目