题目内容
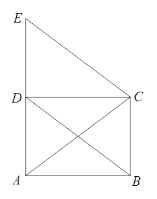
【题目】如图,直线l1的表达式为:y=-3x+3,且直线l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,求点P的坐标.

【答案】(1)(1,0);(2)![]() ;(3)
;(3)![]() ;(4)(6,3).
;(4)(6,3).
【解析】
(1)由题意已知l1的解析式,令y=0求出x的值即可;
(2)根据题意设l2的解析式为y=kx+b,并由题意联立方程组求出k,b的值;
(3)由题意联立方程组,求出交点C的坐标,继而即可求出S△ADC;
(4)由题意根据△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离进行分析计算.
解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,y=![]() ,代入表达式y=kx+b,
,代入表达式y=kx+b,
∴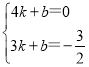 ,
,
∴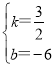 ,
,
∴直线l2的解析表达式为![]() ;
;
(3)由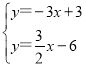 ,解得
,解得![]() ,
,
∴C(2,-3),
∵AD=3,
∴![]() ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x-6,y=3,
∴1.5x-6=3,解得x=6,
所以P(6,3).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目