题目内容
【题目】已知二次函数y=-x2-2x+3.
(1)将其配方成y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标.
(2)在平面直角坐标系中画出函数的图象,并观察图象,当y≥0时,x的取值范围.
【答案】(1)y=-(x+1)2+4;开口向下,对称轴是直线x=-1,顶点坐标为(-1,4);(2)图像见解析;y≥0时,-3≤x≤1.
【解析】
(1)根据题目中的函数解析式,利用配方法可以将题目中的函数解析式化为y=a(x-k)2+h的形式,并写出它的开口方向、对称轴及顶点坐标;
(2)根据题目中的函数解析式可以画出函数的图象,并直接写出当y≥0时,x的取值范围.
(1)二次函数y=-x2-2x+3=-(x+1)2+4,
故该函数的开口向下,对称轴是直线x=-1,顶点坐标为(-1,4);
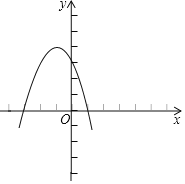
(2)当y=0时,0=-x2-2x+3,得x=-3或x=1,
故该函数的图象如右图所示,
当y≥0时,x的取值范围是-3≤x≤1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目