题目内容
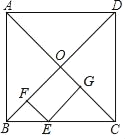
【题目】如图,在正方形ABCD中,边长为4,对角线AC、BD交于点O,点E是BC边上任意一点,分别向BD、AC作垂线,垂足分别为F、G,则四边形OFEG的周长是_____.
【答案】![]()
【解析】
先证明四边形OFEG是矩形,再证四边形OFEG的周长=OB+OC即可解决问题;
解:∵四边形ABCD是正方形,AB=4,
∴AC⊥BD,OB=OC=2![]() ,∠OBC=∠OCB=45°,
,∠OBC=∠OCB=45°,
∵EF⊥OB,EG⊥OC,
∴∠EFO=∠FOG=∠EGO=90°,
∴四边形OFEG是矩形,
∴OF=EG,EF=OG,
∵△EFB,△EGC都是等腰直角三角形,
∴EF=FB,GE=GC,
∴四边形OFEG的周长=OF+FE+OG+GE=OF+FB+OG+GC=OB+OC=4![]() ,
,
故答案为4![]() .
.

练习册系列答案
相关题目