题目内容
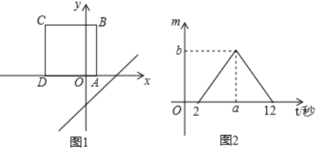
【题目】如图,小明同学将五个正方形按图1所示位置摆放后发现中间空白处是边长为3的小正方形,根据这个信息,小明设右下角的最小的正方形边长为x:
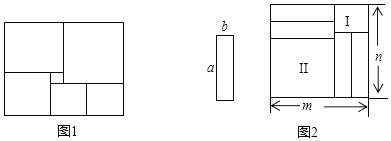
(1)则右上角最大的正方形边长为 ;
(2)求拼成的大长方形的长和宽分别为多少?
(3)小明又将四个长为a,宽为b的小长方形放到图2中的长方形中,得到如图2所示的图形,则图形Ⅰ和图形Ⅱ的周长之和是 .
【答案】(1)(x+9);(2)长为39,宽为33;(3)4n
【解析】
(1)最右下角的小正方形与它左边的小正方形边长同为x,从下方中间的小正方形开始顺时针数过去,每一个都比前一个边长大3.
(2)用不同方法表示AD和EG,列方程求出x,即可求出大长方形的长和宽.
(3)用m、n表示图形Ⅰ和图形Ⅱ的长宽,然后计算即可.
解:(1)如图1,∵AB=BC=x,
∴CD=x+3,
∴EF=x+3+3=x+6,
∴FG=x+6+3=x+9,
故答案为:(x+9);
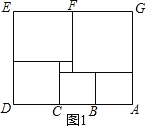
(2)由(1)得:AD=x+x+x+3=3x+3,EG=x+6+x+9=2x+15,
∵AD=EG,
∴3x+3=2x+15,
解得:x=12,
∴AD=3x+3=39,DE=x+3+x+6=2x+9=33,
∴长方形长为39,宽为33;
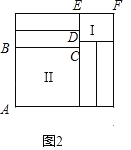
(3)如图,AB=n﹣2b,BC=a,DE=n﹣a,EF=2b,
∴C=2(AB+BC)+2(DE+EF)=2(n﹣2b+a)+2(n﹣a+2b)=4n.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目