题目内容
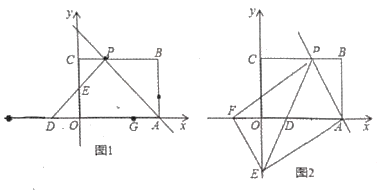
【题目】如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)若![]() 为等腰直角三角形.
为等腰直角三角形.
①直接写出此时![]() 点的坐标:______;直线
点的坐标:______;直线![]() 的解析式为______;
的解析式为______;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(Ⅱ)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
【答案】(1)①![]() ,
, ![]() ;②
;②![]() 周长的最小值为
周长的最小值为![]() ;(Ⅱ)直线
;(Ⅱ)直线![]() 解析式
解析式![]() .
.
【解析】
(1)①直接根据条件就可以求出点和解析式.
②作![]() 点关于
点关于![]() 轴对称点
轴对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 对称点
对称点![]() 连接
连接![]() 交
交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() ,求出直线
,求出直线![]() 解析式,再根据条件求出最小周长.
解析式,再根据条件求出最小周长.
(2) 作![]() 于
于![]() ,,先求出
,,先求出![]() ,再求出E,P两点的坐标,再列解析式.
,再求出E,P两点的坐标,再列解析式.
(1)①![]() ,∴直线
,∴直线![]() 解析式
解析式![]() ;
;
②作![]() 点关于
点关于![]() 轴对称点
轴对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 对称点
对称点![]() 连接
连接![]() 交
交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() ,此时
,此时![]() 周长的最小,
周长的最小,
∵![]() ,
,![]() ,
,
∴直线![]() 解析式
解析式![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 周长的最小值为
周长的最小值为![]() ;
;
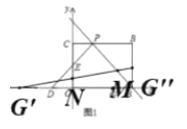
(Ⅱ)如图:作![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设直线![]() 的解析式
的解析式![]() ,
,
![]() ,
,
∴![]() ,
,
∴直线![]() 解析式
解析式![]() .
.


练习册系列答案
相关题目