Question

【题目】补全解答过程：

（1）如图，线段AC=4，线段BC=9，点M是AC的中点，在CB上取一点N，CN：NB=1:2，求MN的长．

解：∵M是AC的中点，AC=4，

∴MC= （填线段名称）= ，

又因为CN：NB=1：2，BC=9，

∴CN= （填线段名称）= ．

∴MN= （填线段名称）+ （填线段名称）=5．

∴MN的长为5．

（2）已知：如图，直线AB∥CD，直线EF与直线AB，CD分别交于点G，H；GM平分∠FGB，∠3＝60°．求∠1的度数．

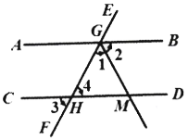
解：∵EF与CD交于点H，（已知）

∴∠3＝∠4．（ ）

∵∠3＝60°，（ ）

∴∠4＝60°．

∵AB∥CD，EF与AB，CD交于点G，H，（已知）

∴∠4+∠FGB＝180°．（ ）

∴∠FGB＝ ．

∵GM平分∠FGB，（已知）

∴∠1＝ °．（角平分线的定义）

Answer 1

【答案】（1）AC；2；BC；3；MC；NC；（2）对顶角相等；已知；两直线平行，同旁内角互补；120°；60．

【解析】

(1) 根据线段中点的性质，可得MC的长，根据线段长度的比，可得CN的长，根据线段的和差，可得答案；

(2) 依据对顶角相等以及平行线的性质，即可得到∠4=60°，∠FGB=120°，再根据角平分线的定义，即可得出∠1=60°．

（1） 解：∵M是AC的中点，AC=4，
∴MC=AC=2，
又因为CN：NB=1：2，BC=9，
∴NC=BC=3．
∴MN=MC+NC=5．
∴MN的长为5．
故答案为：AC；2；BC；3；MC；NC．

（2） 解：∵EF与CD交于点H，（已知）
∴∠3=∠4．（对顶角相等）
∵∠3=60°，（已知）
∴∠4=60°．
∵AB∥CD，EF与AB，CD交于点G，H，（已知）
∴∠4+∠FGB=180°．（两直线平行，同旁内角互补）
∴∠FGB=120°．
∵GM平分∠FGB，（已知）
∴∠1=60°．（角平分线的定义）
故答案为：对顶角相等；已知；两直线平行，同旁内角互补；120°；60．