题目内容
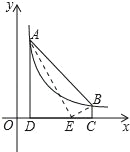
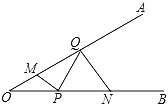
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是_____.
【答案】2![]()
【解析】
作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值;证出△ONN′为等边三角形,△OMM′为等边三角形,得出∠N′OM′=90°,由勾股定理求出M′N′即可.
作M关于OB的对称点M′,作N关于OA的对称点N′,如图所示:

连接M′N′,即为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴∠N′OM′=90°,
∴在Rt△M′ON′中,
M′N′=![]() .
.
故答案为:2![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
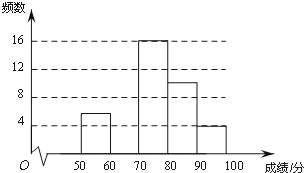
【题目】为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 | a | 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | c | b |
合计 | 50 | 1.00 |
(1)表中的a=______,b=______,c=______;
(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.