题目内容
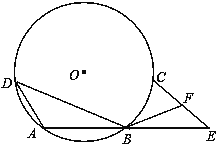
【题目】如图,已知:∠C=∠D,OD=OC.求证:DE=CE.

【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
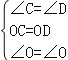 ,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
 ,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27
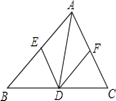
【题目】如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.

【答案】(1)75°(2)证明见解析
【解析】试题分析:(1)根据已知条件易证△ADC≌△BDE,根据全等三角形的性质可得BE=AC=BC,∠EBD=∠CAD=15°,根据等腰三角形的性质和三角形的内角和定理即可求得∠BCE的大小;(2)由(1)中的△ADC≌△BDE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)∵△ACB是等腰直角三角形,
∴AC=BC,∠CAB=∠CBA=45°
∵△ABD和△DEC是等边三角形,
∴AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°
∴∠DAC=60°﹣45°=15°,∠DBC=15°,∠EDB=∠CDA=60°﹣∠BCD,
在△ADC和△BDE中
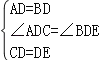
∴△ADC≌△BDE,
∴BE=AC=BC,∠EBD=∠CAD=15°,
∴∠BCE=∠BEC=![]() (180°﹣15°﹣15°)=75°;
(180°﹣15°﹣15°)=75°;
(2)证明:∵△ADC≌△BDE,
∴BE=AC.

【题目】已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天 | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?