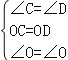题目内容
【题目】(10分)如图,已知⊙O上依次有A、B、C、D四个点,![]() =
=![]() ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)求证:BF=![]() BD;
BD;
(2)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
【答案】(1)证明见解析;(2)存在,作图略;PG=PF.
【解析】试题分析:(1)利用三角形中位线定理得出BF=![]() AC,再利用圆心角定理得出
AC,再利用圆心角定理得出![]() =
=![]() ,进而得出BF=
,进而得出BF=![]() BD;
BD;
(2)首先过点B作AE的垂线,与⊙O的交点即为所求的点P,得出BP⊥AE,进而证明△PBG≌△PBF(SAS),求出PG=PF.
试题解析:(10分)
(1)证明:连接AC,
∵AB=BE,∴点B为AE的中点,
∵F是EC的中点,∴BF为△EAC的中位线,∴BF=![]() AC,
AC,
∵![]() =
=![]() ,∴
,∴![]() +
+![]() =
=![]() +
+![]() ,∴
,∴![]() =
=![]() ,∴BD=AC,∴BF=
,∴BD=AC,∴BF=![]() BD;
BD;
(2)解:过点B作AE的垂线,与⊙O的交点即为所求的点P,
∵BF为△EAC的中位线,∴BF∥AC,∴∠FBE=∠CAE,
∵![]() =
=![]() ,∴∠CAB=∠DBA,
,∴∠CAB=∠DBA,
∵由作法可知BP⊥AE,∴∠GBP=∠FBP,
∵G为BD的中点,∴BG=![]() BD,∴BG=BF,
BD,∴BG=BF,
在△PBG和△PBF中,
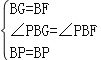 ,
,
∴△PBG≌△PBF(SAS),∴PG=PF.


【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)