题目内容
如图,已知△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2cm,则BC的长为 。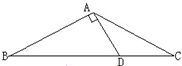

6cm
试题分析:首先根据AB=AC,可得∠B的度数,再求出∠DAC的度数,然后根据直角三角形的性质可得到BD的长,再根据等角对等边可得到CD的长,进而可得到答案.
∵AB=AC,∠C=30°,
∴∠B=∠C=30°,
∴∠BAC=120°,
∵AB⊥AD,AD=2cm,
∴∠BAD=90°,BD=2AD=4cm,
∴∠DAC=120°-90°=30°,
∴AD=CD=2cm,
∴CB=DB+CD=6cm.
点评:解答本题的关键是熟练掌握在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
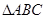 中,点
中,点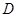 为
为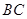 边上的一点,
边上的一点,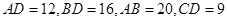 .
.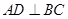 .
.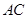 的长及
的长及
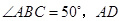 垂直平分线段
垂直平分线段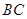 于点
于点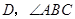 的平分线
的平分线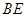 交
交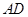 于点
于点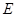 ,连结
,连结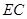 , 则
, 则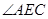 的度数是 .
的度数是 .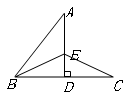
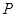 的距离是()
的距离是()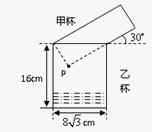
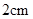
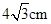
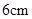
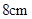
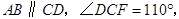 且
且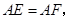 求
求 的度数.
的度数.