Question

【题目】△ABC中，AB=12，AC= ，∠B=30°，则△ABC的面积是 ．

Answer 1

【答案】21 或15
【解析】解：①如图1，作AD⊥BC，垂足为点D，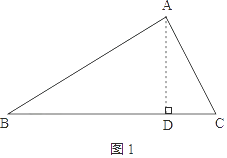

在Rt△ABD中，∵AB=12、∠B=30°，
∴AD= AB=6，BD=ABcosB=12× =6 ，
在Rt△ACD中，CD= = = ，
∴BC=BD+CD=6 + =7 ，
则S△ABC= ×BC×AD= ×7 ×6=21 ；
②如图2，作AD⊥BC，交BC延长线于点D，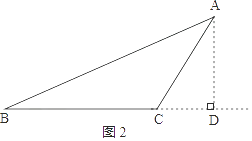

由①知，AD=6、BD=6 、CD= ，
则BC=BD﹣CD=5 ，
∴S△ABC= ×BC×AD= ×5 ×6=15 ，
故答案为：21 或15 ．
由在直角三角形中，30度角所对的边是斜边的一半和余弦的定义，求出AD、BD=ABcosB的值，再由勾股定理求出BC=BD+CD的值，得到S△ABC的面积.