题目内容
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠APC与∠BAP、∠PCD之间的关系.

解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
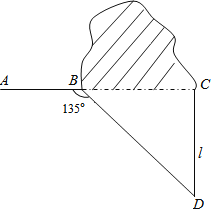
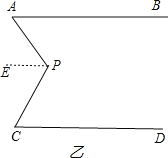
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠APC与∠BAP、∠PCD之间的关系.
【答案】见解析
【解析】
图乙,过P作PE∥AB,求出AB∥PE∥CD,根据平行线的性质得出∠A=∠APE,∠C=∠CPE,即可求出答案;
图丙,根据平行线的性质得出∠PCD=∠POB,根据三角形外角性质求出∠POB=∠PAB+∠APC,即可求出答案.
解:图乙,∠APC=∠A+∠C,
理由是:
过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠A=∠APE,∠C=∠CPE,
∴∠APC=∠APE+∠CPE=∠A+∠C;
图丙,∠APC=∠PCD-∠PAB,
理由是:∵AB∥CD,
∴∠PCD=∠POB,
∵∠POB=∠PAB+∠APC,
∴∠APC=∠POB-∠PAB=∠PCD-∠PAB.

练习册系列答案
相关题目