题目内容
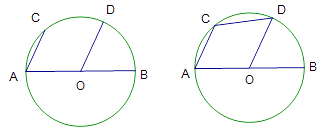
【题目】如图,![]() 为矩形
为矩形![]() 的对角线,将边
的对角线,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,将边
处,将边![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处.
处.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 求四边形
求四边形![]() 的面积及
的面积及![]() 与
与![]() 之间的距离.
之间的距离.
【答案】(1)证明见解析;(2)面积为30,距离为![]() .
.
【解析】
(1)根据矩形的性质可得![]() 从而得出
从而得出![]() ,然后根据折叠的性质可得
,然后根据折叠的性质可得![]() ,从而证出
,从而证出![]() 然后根据平行四边形的定义即可证出结论;
然后根据平行四边形的定义即可证出结论;
(2)根据勾股定理即可求出BC,从而求出CM,设![]() ,然后利用勾股定理列出方程即可求出CE和BE,然后根据平行四边形的面积公式即可求出面积,然后根据勾股定理求出AE,再根据平行四边形的面积公式即可求出
,然后利用勾股定理列出方程即可求出CE和BE,然后根据平行四边形的面积公式即可求出面积,然后根据勾股定理求出AE,再根据平行四边形的面积公式即可求出![]() 与
与![]() 之间的距离.
之间的距离.
![]() 证明:
证明:![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
由折叠的性质可得![]() ,
,
又![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() 在
在![]() 中,
中,![]()
则根据勾股定理得:![]() .
.
![]()
![]() .
.
设![]() ,则
,则![]()
在![]() 中,利用勾股定理可得
中,利用勾股定理可得![]()
即![]() ,
,
解得![]()
∴CE=5,BE=3
故四边形![]() 的面积
的面积![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
设![]() 与
与![]() 之间的距离为
之间的距离为![]()
则![]() ,
,
即![]() ,
,
![]()

练习册系列答案
相关题目