题目内容
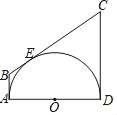
【题目】长方形![]() 中,
中,![]() ,
,![]()
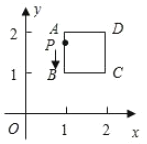
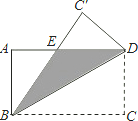
(1)如图1,将该长方形沿对角线![]() 折叠,求△BDE的周长?写出解题过程;
折叠,求△BDE的周长?写出解题过程;
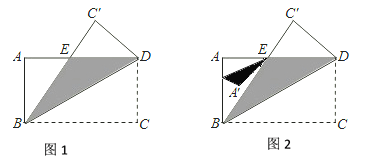
(2)如图2,F是线段AB上的一个动点,在(1)的条件下,再将△AEF沿EF折叠,当A的对应点![]() 恰好落在BE上时,线段AF的值是 (直接写出答案)
恰好落在BE上时,线段AF的值是 (直接写出答案)
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据矩形及折叠的性质可得![]() ,
,![]() ,从而求得
,从而求得![]() ,设设
,设设![]() ,然后利用勾股定理列方程求解DE和BD的长度,从而求得三角形周长;
,然后利用勾股定理列方程求解DE和BD的长度,从而求得三角形周长;
(2)根据矩形和折叠的性质,可得∠F A′B=∠A=90°,AF= A′F,AE= A′E=![]() ,设AF= A′F=a, 在Rt△A′BF中,利用勾股定理列方程求解.
,设AF= A′F=a, 在Rt△A′BF中,利用勾股定理列方程求解.
解:(1)四边形![]() 是长方形,
是长方形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
由折叠的性质可得:![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得:![]() , 即
, 即![]() ,
,
Rt△BCD中,![]()
∴△BDE的周长为![]() ;
;
(2)由(1)可得BE=![]()
∴AE=![]()
将△AEF沿EF折叠,当A的对应点A′恰好落在BE上时
∠F A′B=∠A=90°,AF= A′F,AE= A′E=![]()
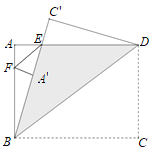
设AF= A′F=a,则BF=3-a,A′B=![]()
在Rt△A′BF中,A′F+ A′B=BF
∴![]()
解得:![]()
∴线段AF的值是![]() .
.

练习册系列答案
相关题目