题目内容
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() .
.
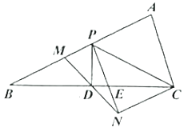
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由“ASA”可证△BMD≌△CND,可得BD=CD,由线段垂直平分线的性质可得PB=PC;
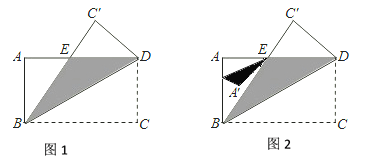
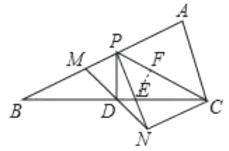
(2)如图,在PC上取点F,使CF=CN,连接EF,由“SAS”可证△CEN≌△CEF,可得EN=EF,∠CNP=∠CFE,由等腰三角形的判定可得EN=EF=PF,即可得结论.
证明:(1)∵CN∥AB,
∴∠B=∠BCN,∠BMD=∠CND,且BM=CN,
∴△BMD≌△CND(ASA)
∴BD=CD,且PD⊥BC,
∴PB=PC;
(2)如图,在PC上取点F,使CF=CN,连接EF,
∵PB=PC,
∴∠PCB=∠B,
∴∠PCB=∠NCB,且CF=CN,CE=CE,
∴△CEN≌△CEF(SAS),
∴EN=EF,∠CNP=∠CFE,
∵∠CFE=∠CPN+∠PEF,∠CNP=2∠CPN,
∴∠CPE=∠PEF,
∴PF=EF,
∴EN=EF=PF,
∵BP=PC,BM=CN=CF,
∴PM=PF=EN.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时, |
当21≤x≤30时, |
(1)请计算第15天该商品单价为多少元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?