Question

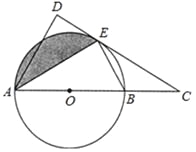
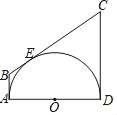
【题目】如图，AB、CD分别与半圆OO切于点A，D，BC切⊙O于点E．若AB=4，CD=9，则⊙O的半径为（　　）

A. 12 B. C. 6 D. 5

Answer 1

【答案】C

【解析】

过B作CD的垂线，设垂足为F；由切线长定理知：BA=BE，CE=CD；即BC=AB+CD；在构建的Rt△BFC中，BC=AB+CD，CF=CD-AB，根据勾股定理即可求出BF即圆的直径，进而可求出⊙O的半径

过B作BF⊥CD于F，

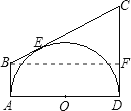
∵AB、CD与半圆O切于A、D，

∴∠BAD=∠CDA=∠BFD=90°，

∴四边形ADFB为矩形，

∴AB=DF，BF=AD，

∵AB=BE=4，CD=CE=9；

∴BC=BE+CE=13；

∵AB、CD与半圆O相切，

∴四边形ADFB为矩形；

∴CF=CD-FD=9-4=5，

在Rt△BFC中，BF===12，

∴AD=BF=12，

∴⊙O的半径为6．

故选：C．