题目内容
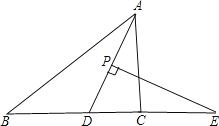
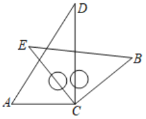
【题目】将一副三角板中的两块直角三角尺的直角顶点![]() 按如图所示的方式叠放在一起(其中
按如图所示的方式叠放在一起(其中![]() ,
,![]() ,
,![]() ),固定三角板
),固定三角板![]() ,另一三角板
,另一三角板![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 顺时针旋转,设旋转的角度为
顺时针旋转,设旋转的角度为![]() .
.
(1)当![]() 时;
时;
①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,求
,求![]() 的度数;
的度数;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出
时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出![]() 所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
【答案】(1)①150°;②50°;(2)∠ACB+∠DCE=180°,理由见详解;(3)当![]() =30°时,AD⊥CE,当
=30°时,AD⊥CE,当![]() =90°时,AC⊥CE,当
=90°时,AC⊥CE,当![]() =75°时,AD⊥BE,当
=75°时,AD⊥BE,当![]() =45°时,CD⊥BE.
=45°时,CD⊥BE.
【解析】
(1)①先根据直角三角板的性质求出∠DCB的度数,进而可得出∠ACB的度数;②由∠ACB=130°,∠ACD=90°,可得出∠DCB的度数,进而得出∠DCE的度数;
(2)根据(1)中的结论可提出猜想,再分3种情况:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别证明∠ACB与∠DCE的数量关系,即可;
时,分别证明∠ACB与∠DCE的数量关系,即可;
(3)分4种情况:①若AD⊥CE时,②若AC⊥CE时, ③若AD⊥BE时,④若CD⊥BE时,分别求出![]() 的值,即可.
的值,即可.
(1)①∵∠ECB=90°,∠DCE=30°,
∴∠DCB=90°30°=60°,
∴∠ACB=∠ACD+∠DCB=90°+60°=150°,
故答案是150°;
②∵∠ACB=130°,∠ACD=90°,
∴∠DCB=130°90°=40°,
∴∠DCE=90°40°=50°;
(2)∠ACB+∠DCE=180°,理由如下:
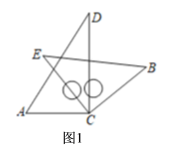
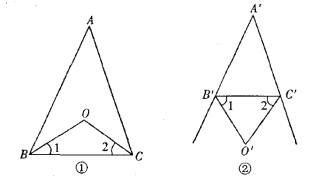
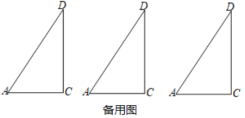
①当![]() 时,如图1,
时,如图1,
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°;
②当![]() 时,如图2,∠ACB+∠DCE=180°,显然成立;
时,如图2,∠ACB+∠DCE=180°,显然成立;
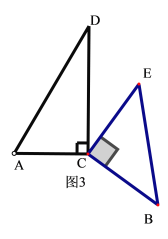
③当![]() 时,如图3,∠ACB+∠DCE=360°-90°-90°=180°.
时,如图3,∠ACB+∠DCE=360°-90°-90°=180°.
综上所述:∠ACB+∠DCE=180°;
(3)存在,理由如下:
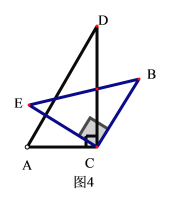
①若AD⊥CE时,如图4,则![]() =90°-∠A=90°-60°=30°,
=90°-∠A=90°-60°=30°,
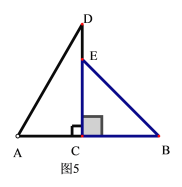
②若AC⊥CE时,如图5,则![]() =∠ACE=90°,
=∠ACE=90°,
③若AD⊥BE时,如图6,则∠EMC=90°+30°=120°,
∵∠E=45°,
∴∠ECD=180°-45°-120°=15°,
∴![]() =90°-15°=75°,
=90°-15°=75°,
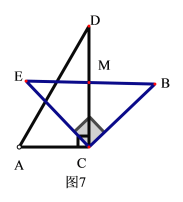
④若CD⊥BE时,如图7,则AC∥BE,
∴![]() =∠E=45°.
=∠E=45°.
综上所述:当![]() =30°时,AD⊥CE,当
=30°时,AD⊥CE,当![]() =90°时,AC⊥CE,当
=90°时,AC⊥CE,当![]() =75°时,AD⊥BE,当
=75°时,AD⊥BE,当![]() =45°时,CD⊥BE.
=45°时,CD⊥BE.