题目内容
【题目】如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x2﹣4x﹣2经过A，B两点．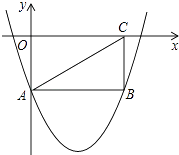
（1）求A点坐标及线段AB的长；
（2）若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒．
①当PQ⊥AC时，求t的值；
②当PQ∥AC时，对于抛物线对称轴上一点H，∠HOQ＞∠POQ，求点H的纵坐标的取值范围．
【答案】
（1）
解：由抛物线y=x2﹣4x﹣2知：当x=0时，y=﹣2，
∴A（0，﹣2）．
由于四边形OABC是矩形，所以AB∥x轴，即A、B的纵坐标相同；
当y=﹣2时，﹣2=x2﹣4x﹣2，解得x1=0，x2=4，
∴B（4，﹣2），
∴AB=4
（2）
解：①由题意知：A点移动路程为AP=t，
Q点移动路程为7（t﹣1）=7t﹣7．
当Q点在OA上时，即0≤7t﹣7＜2，1≤t＜ 
时，
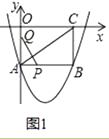
如图1，若PQ⊥AC，则有Rt△QAP∽Rt△ABC．
∴ 
，即 
，
∴t= 
．
∵ ＞ ，
∴此时t值不合题意．
当Q点在OC上时，即2≤7t﹣7＜6， ≤t＜ 
时，
如图2，过Q点作QD⊥AB．
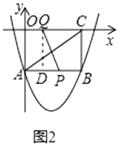
∴AD=OQ=7（t﹣1）﹣2=7t﹣9．
∴DP=t﹣（7t﹣9）=9﹣6t．
若PQ⊥AC，易证Rt△QDP∽Rt△ABC，
∴ 
，即 
= 
，∴t= 
，
∵ ＜ ＜ ，
∴t= 符合题意．
当Q点在BC上时，即6≤7t﹣7≤8， ≤t≤ 
时，
如图3，若PQ⊥AC，过Q点作QG∥AC，
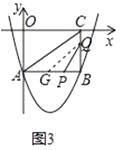
则QG⊥PG，即∠GQP=90°．
∴∠QPB＞90°，这与△QPB的内角和为180°矛盾，
此时PQ不与AC垂直．
综上所述，当t= 时，有PQ⊥AC．
②当PQ∥AC时，如图4，△BPQ∽△BAC，
∴ 
，
∴ 
= 
，
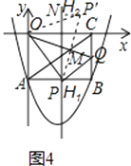
解得t=2，即当t=2时，PQ∥AC．
此时AP=2，BQ=CQ=1，
∴P（2，﹣2），Q（4，﹣1）．
抛物线对称轴的解析式为x=2，
当H1为对称轴与OP的交点时，
有∠H1OQ=∠POQ，
∴当yH＜﹣2时，∠HOQ＞∠POQ．
作P点关于OQ的对称点P′，连接PP′交OQ于点M，
过P′作P′N垂直于对称轴，垂足为N，连接OP′，
在Rt△OCQ中，∵OC=4，CQ=1．
∴OQ= 
，
∵S△OPQ=S四边形ABCO﹣S△AOP﹣S△COQ﹣S△QBP=3= 
OQ×PM，
∴PM= 
，
∴PP′=2PM= 
，
∵对应角的边相互垂直，
∴∠NPP′=∠COQ．
∴△COQ∽△NPP′
∴ 
，
∴P′N= 
，PN= 
，
∴P′（ 
， 
），
∴直线OP′的解析式为y= 
x，
∴OP′与NP的交点H2（2， 
）．
∴当yH＞ 时，∠HOQ＞∠POQ．
综上所述，当yH＜﹣2或yH＞ 时，∠HOQ＞∠POQ．
【解析】（1）已知抛物线的解析式，将x=0代入即可得A点坐标；由于四边形OABC是矩形，那么A、B纵坐标相同，代入该纵坐标可求出B点坐标，则AB长可求．（2）①Q点的位置可分：在OA上、在OC上、在CB上 三段来分析，若PQ⊥AC时，很显然前两种情况符合要求，首先确定这三段上t的取值范围，然后通过相似三角形（或构建相似三角形），利用比例线段来求出t的值，然后由t的取值范围将不合题意的值舍去；②当PQ∥AC时，△BPQ∽△BAC，通过比例线段求出t的值以及P、Q点的坐标，可判定P点在抛物线的对称轴上，若P、H1重合，此时有∠H1OQ=∠POQ，显然若做点H1关于OQ的对称点H2 ， 那么亦可得到∠H2OQ=∠POQ，而题干要求的是∠HOQ＞∠POQ，那么H1点以下、H2点以上的H点都是符合要求的．
【考点精析】本题主要考查了二次函数的性质和抛物线与坐标轴的交点的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．
