题目内容
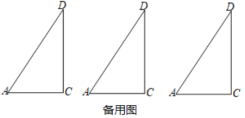
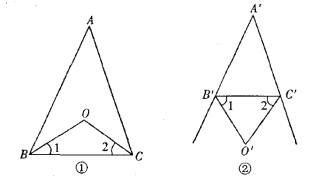
【题目】(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
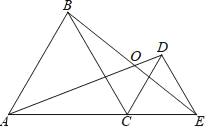
(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;
(3)上面(1)(2)两题中的∠BOC与∠B′O′C′ 有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′ 是否还具有这样的关系?这个结论你是怎样得到的?
【答案】(1)110° ; (2)70° ; (3)互补.
【解析】
(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据BO、CO分别平分∠ABC与∠ACB求出∠OBC+∠OCB的度数,由三角形内角和定理即可得出∠BOC的度数.
(2)利用三角形的内角和以及外角和性质即可进行解答;
(3)根据三角形内角和定理和角平分线定义,(3)由前两问提供的思路,进一步推理.
解:(1)∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°.
∵BO、CO分别是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×140°=70°,
×140°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°;
(2)因为∠A的外角等于180°-40°=140°,
△A′B′C′另外的两外角平分线相交于点O′,
根据三角形的外角和等于360°,
所以∠1+∠2=![]() ×(360°-140°)=110°,
×(360°-140°)=110°,
∠B′O′C′=180°-110°=70°;
(3)∵(1)(2)中∠BOC+∠B′O′C′=110°+70°=180°,∴∠BOC与∠B′O′C′互补;
证明:当∠A=n°时,∠BOC=180°-[(180°-n°)÷2]=90°+![]() ,
,
∵∠A′=n°,∠B′O′C′=180°-[360°-(180°-n°)]÷2=90°-![]() ,
,
∴∠A+∠A′=90°+![]() +90°-
+90°-![]() =180°,∠BOC与∠B′O′C′互补,
=180°,∠BOC与∠B′O′C′互补,
所以当∠A=∠A′=n°,∠BOC与∠B′O′C′还具有互补的关系.

 阅读快车系列答案
阅读快车系列答案【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
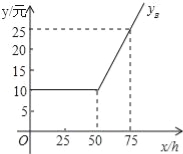
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?