��Ŀ����
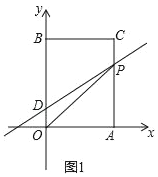
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪OA=6��OB=10����DΪy����һ�㣬������Ϊ��0��2������P�ӵ�A������ÿ��2����λ���ٶ����߶�AC��CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮
(1)����P������Cʱ����ֱ��DP�ĺ�������ʽ��
(2)�����OPD�����S����t�ĺ�������ʽ��
����ͼ�ڣ��ѳ���������OP�۵�����B�Ķ�Ӧ��B��ǡ������AC���ϣ����P�����꣮
(3)��P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��![]() x+2����2����S��6��S����2t+16������P�������ǣ�
x+2����2����S��6��S����2t+16������P�������ǣ�![]() ��10������3�����ڣ����������P����Ϊ��6��6����6��2
��10������3�����ڣ����������P����Ϊ��6��6����6��2![]() +2����6��10��2
+2����6��10��2![]() ����
����
��������
��1����ֱ��DP����ʽΪy=kx+b����D��C����������k��b��ֵ������ȷ��������ʽ��
��2������P��AC��ʱ����ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ��
����D����OP�ĶԳƵ�����x����ʱ��ֱ��OPΪy=x�������ʱP���꼴�ɣ�
��3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
�⣺��1����OA��6��OB��10���ı���OACBΪ�����Σ�
��C��6��10����
���ʱֱ��DP����ʽΪy��kx+b��
�ѣ�0��2����C��6��10���ֱ���룬��
![]() ��
��
���![]()
���ʱֱ��DP����ʽΪy��![]() x+2��
x+2��
��2��������P���߶�AC��ʱ��OD��2����Ϊ6��S��6��
����P���߶�BC��ʱ��OD��2����Ϊ6+10��2t��16��2t��S��![]() ��2����16��2t������2t+16��
��2����16��2t������2t+16��
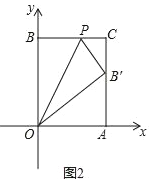
����P��m��10������PB��PB�䣽m����ͼ2��
��OB�䣽OB��10��OA��6��
��AB�䣽![]() ��8��
��8��
��B��C��10��8��2��
��PC��6��m��
��m2��22+��6��m��2�����m��![]()
���ʱ��P�������ǣ�![]() ��10����
��10����
��3�����ڣ�����Ϊ��
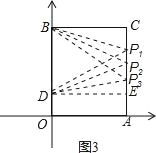
����BDPΪ���������Σ�������������ǣ���ͼ3��
����BD��BP1��OB��OD��10��2��8��
��Rt��BCP1��BP1��8��BC��6��
���ݹ��ɶ����ã�CP1��![]() ��2
��2![]() ��
��
��AP1��10��2![]() ����P1��6��10��2
����P1��6��10��2![]() ����
����
����BP2��DP2ʱ����ʱP2��6��6����
����DB��DP3��8ʱ��
��Rt��DEP3��DE��6��
���ݹ��ɶ����ã�P3E��![]() ��2
��2![]() ��
��
��AP3��AE+EP3��2![]() +2����P3��6��2
+2����P3��6��2![]() +2����
+2����
���ϣ����������P����Ϊ��6��6����6��2![]() +2����6��10��2
+2����6��10��2![]() ����
����
�㾦����������һ�κ����ۺ��⣬�漰��֪ʶ�У�����ϵ����ȷ��һ�κ�������ʽ��������ͼ�����ʣ����������εĶ��壬���ɶ����������˷������۵�˼�룬�������մ���ϵ�����ǽⱾ���һ�ʵĹؼ���

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�