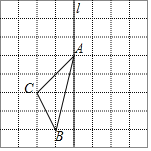
题目内容
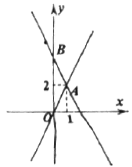
【题目】如图,∠A=∠B=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.
(1)求证:△APM≌△BPN;
(2)当MN=2BN时,求α的度数;
(3)若△BPN的外心在该三角形的内部,直接写出α的取值范围.
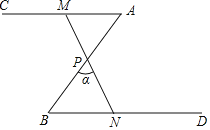
【答案】(1)证明见解析;(2)α=50°;(3)40°<α<90°.
【解析】(1)根据AAS即可证明△APM≌△BPN;
(2)由(1)中的全等得:MN=2PN,所以PN=BN,由等边对等角可得结论;
(3)三角形的外心是外接圆的圆心,三边垂直平分线的交点,直角三角形的外心在直角顶点上,钝角三角形的外心在三角形的外部,只有锐角三角形的外心在三角形的内部,所以根据题中的要求可知:△BPN是锐角三角形,由三角形的内角和可得结论.
(1)∵P是AB的中点,
∴PA=PB,
在△APM和△BPN中,
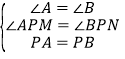 ,
,
∴△APM≌△BPN;
(2)由(1)得:△APM≌△BPN,
∴PM=PN,
∴MN=2PN,
∵MN=2BN,
∴BN=PN,
∴α=∠B=50°;
(3)∵△BPN的外心在该三角形的内部,
∴△BPN是锐角三角形,
∵∠B=50°,
∴40°<∠BPN<90°,即40°<α<90°.

 阅读快车系列答案
阅读快车系列答案【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?