题目内容
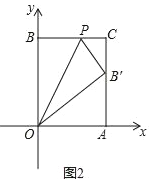
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

【答案】证明见解析
【解析】
(1)根据正方形的性质和全等三角形的判定证明即可;
(2)四边形AECF是菱形,根据对角线垂直的平行四边形是菱形即可判断;
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠DBC,
∵CQ∥DB,
∴∠BCQ=∠DBC,
∵DP=CQ,
∴△ADP≌△BCQ.
(2)证明:∵CQ∥DB,且CQ=DP,
∴四边形CQPD是平行四边形,
∴CD=PQ,CD∥PQ,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴AB=PQ,AB∥PQ,
∴四边形ABQP是平行四边形,
∵△ADP≌△BCQ,
∴∠APD=∠BQC,
∵∠∠APD+∠APB=180°,
∴∠ABP=∠APB,
∴AB=AP,
∴四边形ABQP是菱形.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出![]() =83分,
=83分,![]() =82分,绘制成如下尚不完整的统计图表.
=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
(1)a=
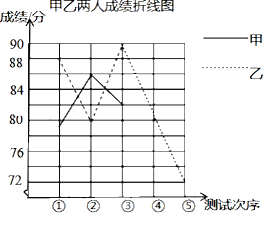
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |

(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?