题目内容
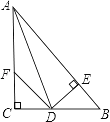
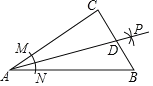
【题目】如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，大于
MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D,若AC＝24，AB＝30，且
＝216，则△ABD的面积是( )
A.105B.120
C.135D.115
【答案】B
【解析】
先利用勾股定理计算出BC=18，作DH⊥AB于H，如图，设DH=x，则BD=18-x，利用作法得AD为∠BAC的平分线，则根据角平分线的性质得CD=DH=x，接着证明△ADC≌△ADH得到AH=AC=24，所以BH=6，然后在Rt△BDH中利用勾股定理得到x，然后根据三角形的面积公式即可得到结论．
解：在Rt△ACB中，
，
作DH⊥AB于H，如图，
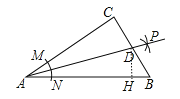
由作法得AD为∠BAC的平分线，设DH=x，
∴CD=DH=x，则BD=18-x，
在Rt△ADC与Rt△ADH中，
，
∴△ADC≌△ADH，(HL)，
∴AH=AC=24，
∴BH=30-24=6，
在Rt△BDH中，
，
解得：
，
∴△ABD的面积
；
故选择：B.
练习册系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
