题目内容
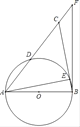
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
【答案】(1)证明见解析;(2)CF=![]() .
.
【解析】
(1)连接BD,由圆周角定理知DB⊥AC,根据等腰三角形三线合一的性质即可证得D是AC的中点.
(2)根据切线的性质得到∠ABF=90°,根据同弧所对的圆周角相等,得到∠CAE=∠CBD,又∠CBD=∠ABD,∠ABD=∠F,则sin∠CAE=sin∠F=sin∠ABD,则
![]() 即可求出
即可求出![]() 的长度,即可求解.
的长度,即可求解.
(1)证明:连接DB,
∴AB是⊙O直径,
∴∠ADB=90°,
∴DB⊥AC.
又∵AB=BC.
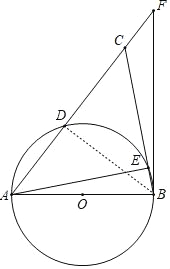
∴D是AC的中点.
(2)解:∵BF与⊙O相切于点B,
∴∠ABF=90°,
∵∠CAE=∠CBD,
∴∠CBD=∠ABD,∠ABD=∠F,
∴sin∠CAE=sin∠F=sin∠ABD,
∴在△ADB和△ABF中, ![]()
∵AB=12,
∴![]()
∴CF=AF﹣AC=![]() -
-![]() =
=![]() .
.

【题目】某企业为了解饮料自动售卖机的销售情况,对甲、乙两个城市的饮料自动售卖机进行抽样调查,从两个城市中所有的饮料自动售卖机中分别抽取16台,记录下某一天各自的销售情况(单位:元)如下:
甲:25、45、38、22、10、28、61、18、38、45、78、45、58、32、16、78
乙:48、52、21、25、33、12、42、39、41、42、33、44、33、18、68、72
整理、描述数据:对销售金额进行分组,各组的频数如下:
销传金额 |
|
|
|
|
甲 | 3 | 6 | 4 | 3 |
乙 | 2 | 6 | a | b |
分析数据:两组样本数据的平均数、中位数如下表所示:
城市 | 中位数 | 平均数 | 众数 |
甲 | C | 39.8 | 45 |
乙 | 40 | 38.9 | d |
请根据以上信息,回答下列问题:
(1)填空:a=, b=, c=, d=.
(2)两个城市目前共有饮料自动售卖机4000台,估计日销售金额不低于40元的数量约为多少台?
(3)根据以上数据,你认为甲、乙哪个城市的饮料自动售卖机销售情况较好?请说明理由(一条理由即可).