题目内容
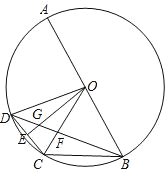
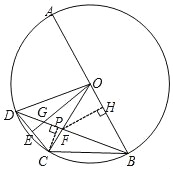
【题目】如图,AB是⊙O的直径,弦BC=OB,点D是![]() 上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
(1)求∠DGE的度数;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)记△CFB,△DGO的面积分别为S1,S2,若![]() =k,求
=k,求![]() 的值.(用含k的式子表示)
的值.(用含k的式子表示)
【答案】(1)∠DGE=60°;(2)![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
(1)根据等边三角形的性质,同弧所对的圆心角和圆周角的关系,可以求得∠DGE的度数;
(2)根据题意,三角形相似、勾股定理可以求得![]() 的值;
的值;
(3)根据题意,作出合适的辅助线,然后根据三角形相似、勾股定理可以用含k的式子表示出![]() 的值.
的值.
解:(1)∵BC=OB=OC,
∴∠COB=60°,
∴∠CDB=![]() ∠COB=30°,
∠COB=30°,
∵OC=OD,点E为CD中点,
∴OE⊥CD,
∴∠GED=90°,
∴∠DGE=60°;
(2)过点F作FH⊥AB于点H
设CF=1,则OF=2,OC=OB=3
∵∠COB=60°
∴OH=![]() OF=1,
OF=1,
∴HF=![]() OH=
OH=![]() ,HB=OB﹣OH=2,
,HB=OB﹣OH=2,
在Rt△BHF中,BF![]() ,
,
由OC=OB,∠COB=60°得:∠OCB=60°,
又∵∠OGB=∠DGE=60°,
∴∠OGB=∠OCB,
∵∠OFG=∠CFB,
∴△FGO∽△FCB,
∴$\frac{O F}{B F}=\frac{G F}{C F}$,
∴GF=$\frac{2}{\sqrt{7}}$,
∴![]() =
=![]() .
.
(3)过点F作FH⊥AB于点H,
设OF=1,则CF=k,OB=OC=k+1,
∵∠COB=60°,
∴OH=![]() OF=
OF=![]() ,
,
∴HF=![]() ,HB=OB﹣OH=k+
,HB=OB﹣OH=k+![]() ,
,
在Rt△BHF中,
BF=![]() ,
,
由(2)得:△FGO∽△FCB,
∴![]() ,即
,即![]() ,
,
∴GO![]() ,
,
过点C作CP⊥BD于点P
∵∠CDB=30°
∴PC=![]() CD,
CD,
∵点E是CD中点,
∴DE=![]() CD,
CD,
∴PC=DE,
∵DE⊥OE,
∴![]() =
=![]() =
= =
=![]()

【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.