题目内容
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且过抛物线
,且过抛物线![]() 的顶点
的顶点![]() 和抛物线上的另一点
和抛物线上的另一点![]() .
.
(1)若点![]()
①求抛物线解析式;
②若![]() ,求直线解析式.
,求直线解析式.
(2)若![]() ,过点
,过点![]() 作
作![]() 轴的平行线与抛物线的对称轴交于点
轴的平行线与抛物线的对称轴交于点![]() ,当
,当![]() 时,求
时,求![]() 的面积
的面积![]() 的最大值.
的最大值.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)根据顶点坐标求出b、 c,即可求出抛物线解析式,由直线与抛物线交于点P得y=kx-2k-2,联立![]() 得
得![]() 的横坐标为
的横坐标为![]() ,根据Q点的纵坐标即可解决问题.
,根据Q点的纵坐标即可解决问题.
(2)由题意可以假设直线PQ=-2x+b′,利用方程组求出点Q坐标,分两种情形①-1≤b≤0时,②-4<b∠-1时,构建二次函数,根据二次函数的性质即可解决问题.
(1)①![]() (的顶点为
(的顶点为![]() ),
),
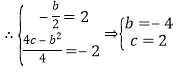 ,
,
![]() ;
;
②![]() 过
过![]() ,
,
![]() ,
,
联立![]()
![]()
![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
![]() 的横坐标为
的横坐标为![]() ,
,
代入![]() ,
,
得![]() ,
,
![]() ,
,
又![]() 且
且![]() ,
,
![]() 的纵坐标为
的纵坐标为![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)设![]() ,
,
![]() 顶点
顶点![]() ,
,
代入上式得![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() ,
,
由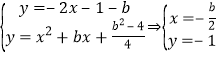 或
或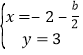 ,
,
![]() ,
,
![]() ,
,
① ![]() 时,
时,
![]() ,
,
![]() ,
,
![]() 时,
时,![]() 面积最大
面积最大![]() ,
,
② ![]() 时,
时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 时,
时,
![]() 面积最大为
面积最大为![]() ,
,
![]() .
.
故答案为:(1)①![]() ;②
;②![]() ;(2)
;(2)![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目