Question

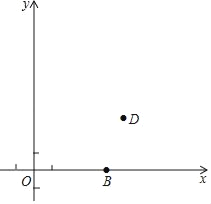
【题目】如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0）和点B，且OB＝3OA，与y轴交于点C，此抛物线顶点为点D．

（1）求抛物线的表达式及点D的坐标；

（2）如果点E是y轴上的一点（点E与点C不重合），当BE⊥DE时，求点E的坐标；

（3）如果点F是抛物线上的一点．且∠FBD＝135°，求点F的坐标．

Answer 1

【答案】（1）D(1,-4)；（2）E（0，1）；（3）（-4，21）.

【解析】

（1）根据已知得出点B的坐标，将A,B坐标代入抛物线解析式，进而确定出抛物线的解析式.再根据解析式求得顶点D的坐标.

（2）设点E坐标为（0，t），根据勾股定理，BE2＋DE2＝BD2，解出t的值，从而得到E点坐标.

（3）构造三角形，求出直线BF的方程式，再由方程式和抛物线解析式求解得点F 的坐标.

⑴ ，

∴D（1，－4）；

⑵ 设E（0，t）,

则,

∴E(0,－1)；

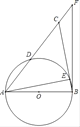
⑶ 又⑵得∠BCD＝90°,

∴△BCD≌△BEG,EG＝CD＝,BE＝BC＝,

∠DBG＝135°,

∴G(,),

又B（3，0），

∴BF:，

∴.

故答案为：（1）D(1，－4)；（2）E（0，1）；（3）（－4，21）