Question

【题目】在平面直角坐标系中，点A（4，0），B为第一象限内一点，且OB⊥AB，OB＝2．

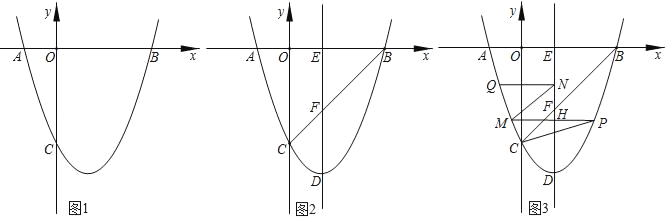
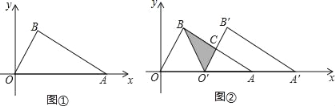
（1）如图①，求点B的坐标；

（2）如图②，将△OAB沿x轴向右平移得到△O′A′B′，设OO′＝m，其中0＜m＜4，连接BO′，AB与O′B′交于点C．

①试用含m的式子表示△BCO′的面积S，并求出S的最大值；

②当△BCO′为等腰三角形时，求点C的坐标（直接写出结果即可）．

Answer 1

【答案】（1）B（1，）；（2）①当m＝2时，S最大＝，②C（，）．

【解析】

(1)由OB⊥AB，0A＝4，OB＝2得出△AOB是有一个角为30°的直角三角形，简单计算即可；

（2）①由平移用m表示出BC，O′C，建立S＝[﹣（m﹣2）2+4]，即可；

②利用△BCO′为等腰三角形，则有CB＝CO′确定出m，再利用相似求出CD，AD即可．

解：（1）∵OB⊥AB，0A＝4，OB＝2，

∴∠AOB＝60°，∠OAB＝30°，AB＝2，

过点B作BE⊥OA，

∴OD＝1，BE＝，

∴B（1，）．

（2）①∵△A′O′B′是△OAB平移得到，

∴∠A′O′B′＝∠AOB＝60°，O′B′⊥AB，

∵OO′＝m，

∴AO′＝4﹣m，

∴O′C＝AO′＝（4﹣m），AC＝AO′＝（4﹣m），

∴BC＝AB﹣AC＝m，

∴S＝BC×O′C＝m（4﹣m）＝ [﹣（m﹣2）2+4]，

当m＝2时，S最大＝．

②如下图，作BE⊥OA，CD⊥OA，

由①有，AO′＝4﹣m，O′C＝（4﹣m），AC＝（4﹣m），

∴CB＝AB﹣AC＝2﹣（4﹣m）＝m，

由平移得，∠ACO′＝∠ABO＝90°，

∵△BCO′为等腰三角形，

∴CB＝O′C，

∴m＝（4﹣m），

∴m＝2（﹣1）．

∵BE×OA＝OB×AB，

∴BE＝＝，

∴AE＝BE＝3，

∵△ACO′∽△ABO，

∴，

∴CD＝×BE＝×＝＝，

∵BE⊥OA，CD⊥OA，

∴BE∥CD，

∴，

∴AD＝×AE＝，

∴OD＝OA﹣AD＝4﹣＝，

∴C（，）．