题目内容
【题目】已知抛物线 y x2 mx 2m 4（m>0）．
（1）证明：该抛物线与 x 轴总有两个不同的交点；
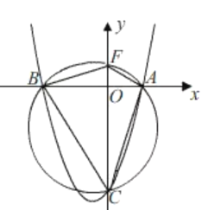
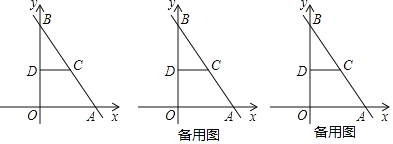
（2）设该抛物线与 x 轴的两个交点分别为 A，B（点 A 在点 B 的右侧)，与 y 轴交于点 C，A，B，三点都在圆 P 上．
①若已知 B（-3，0），抛物线上存在一点 M 使△ABM 的面积为 15，求点 M 的坐标；
②试判断：不论 m 取任何正数，圆 P 是否经过 y 轴上某个定点？若是，求出该定点的坐标，若不是，说明理由．
【答案】（1）见解析；（2）①M
或
或
或
；②是，圆 P经过 y 轴上的定点（0,1）．
【解析】
（1）令y=0，证明
，即可解答；
（2）①将B（-3，0）代入y x2 mx 2m 4，求出抛物线解析式，求出点A的坐标，从而得到AB=5，根据△ABM 的面积为 15，列出方程解答即可；
②求出OA=2，OB=m+2，OC=2（m+2），判断出∠OCB=∠OAF，求出tan∠OCB=
，即可求出OF=1，即可得出结论．
解：（1）当y=0时，x2 mx 2m 4=0
∴
，
∵m>0，
∴
，
∴该抛物线与 x 轴总有两个不同的交点；
（2）①将B（-3，0）代入y x2 mx 2m 4得：
，解得m=1，
∴y x2 x 6，
令y=0得：x2 x 6=0，解得：
，
∴A（2,0），AB=5，
设M（n，n2 n 6）
则
，即
解得：
，
∴M或或或．
②是，圆 P经过 y 轴上的定点（0,1），理由如下：
令y=0，
∴x2 mx 2m 4=0，即
，
∴
或
，
∴A（2,0），
，
∴OA=2，OB=m+2，
令x=0，则y=-2(m+2)，
∴OC=2(m+2)，
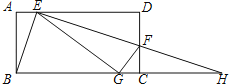
如图，∵点A，B，C在圆P上，
∴∠OCB=∠OAF，
在Rt△BOC中，
，
在Rt△AOF中，
，
∴OF=1，
∴点F（0,1）
∴圆 P经过 y 轴上的定点（0,1）．
