Question

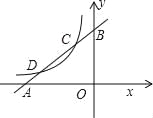
【题目】如图，四边形ABCD为正方形，点A的坐标为(0，2)，点B的坐标为(0，－3)，反比例函数y＝的图象经过点C，一次函数y＝ax＋b的图象经过点A，C.

(1)求反比例函数和一次函数的表达式；

(2)若点P是反比例函数图象上的一点，△AOP的面积恰好等于正方形ABCD的面积，求P点的坐标．

Answer 1

【答案】(1) y＝－ , y＝－x＋2 ;(2) P点坐标为(25，－)或(－25，).

【解析】

试题（1）先根据条件求出点C的坐标，代入y＝可求出k的值，把点Ａ，C坐标代入一次函数解析式y＝ax＋b，然后解方程组可得a，b的值；（2）设点P的坐标为（x，y），根据△OAP的面积恰好等于正方形ABCD的面积，可求出点P的横坐标x，代入反比例函数关系式可求出点P的纵坐标．

试题解析：（1） 因为四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，－3），所以C的坐标为（5，－3），代入y＝可得：k＝－15，所以反比例函数的解析式为；把点Ａ，C坐标代入一次函数解析式得，解得，所以一次函数的解析式为y＝－x＋2；

（2） 设点P的坐标为（x，y），根据△OAP的面积恰好等于正方形ABCD的面积，得：，所以，代入，得或，所以P点的坐标为（25，－）或（－25，）．