Question

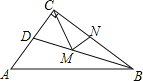
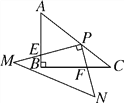
【题目】如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4.Rt△MPN中，∠MPN=90°，点P在AC上，PM交AB于点E，PN交BC于点F，当PE=2PF时，AP=________.

Answer 1

【答案】3

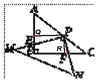
【解析】如图作PQ⊥AB于Q，PR⊥BC于R.

∵∠PQB=∠QBR=∠BRP=90°，

∴四边形PQBR是矩形，

∴∠QPR=90°=∠MPN，

∴∠QPE=∠RPF，

∴△QPE∽△RPF，则==2，

∴PQ=2PR=2BQ.

在Rt△ABC中，AB=3，BC=4，则AC=5.

又∵PQ∥BC，

∴AQ:QP:AP=AB:BC:AC=3:4:5，

设PQ=4x，则AQ=3x，AP=5x，BQ=2x，

∴AQ+BQ=2x+3x=3，得x=，

∴AP=5x=3.

故答案为3.