Question

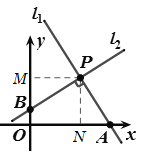
【题目】如图，P点坐标为(2，2)，l1⊥l2，l1.l2分别交x轴和y轴于A点和B点，则四边形OAPB的面积为_______．

Answer 1

【答案】4

【解析】

过点P作PM⊥y轴，PN⊥x轴，垂足分别为M、N，利用AAS证明△APN≌△BPM，从而得四边形OAPB的面积=正方形OMPN的面积，进一步即可求出结果.

解：过点P作PM⊥y轴，PN⊥x轴，垂足分别为M、N，则∠PMB=∠PNA=90°，

∵l1⊥l2，∠MPN=90°，

∴∠APN+∠BPN=90°，∠MPB+∠BPN=90°，

∴∠APN=∠BPM，

∵P点坐标为(2，2)，

∴PN=PM=2，

∴△APN≌△BPM（AAS），四边形OMPN是正方形，

∴四边形OAPB的面积=正方形OMPN的面积=2×2=4.

故答案为4.