题目内容
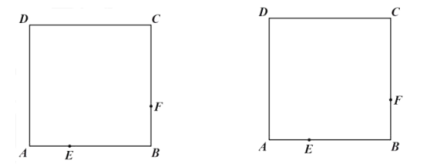
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动;点
时停止运动;点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿着折线
的速度沿着折线![]() 运动,到达点
运动,到达点![]() 时停止运动.点
时停止运动.点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
(2)连接![]() 、
、![]() 交与点
交与点![]() ,
,
①在整个运动过程中,![]() 的最小值为______
的最小值为______![]() ;
;
②当![]() 时,此时
时,此时![]() 的值为______.
的值为______.
【答案】(1)![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() 时,
时,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ;(2)①
;(2)①![]() ;②2或8.
;②2或8.
【解析】
(1)分情况讨论确定E,F的位置,根据勾股定理列式求解即可;
(2)①根据题意分析出点M的运动轨迹是圆,然后即可确定答案;②求证△DAM≌△CDN,△DAE∽△DMA,分情况讨论即可.
(1)当![]() 时,由题可知
时,由题可知![]() ,
,![]() ,
,
∴![]() ,
,
![]() 中,
中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
当![]() 时,由题可知
时,由题可知![]() ,
,![]() ,
,
∴![]() ,
,
![]() 中,
中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
综上所述:![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() 时,
时,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
(2)①![]()
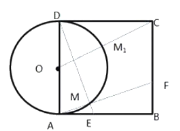
∵E,F两点速度相同,
∴AE=AF
又∵正方形ABCD中,AD=BA,∠DAB=∠B=90°,
∴△DAE≌△BAF(SAS)
∴∠ADE=∠BAF
∵∠BAF+∠DAF=90°
∴∠ADE+∠DAF=90°
∴∠DMA=90°
∴点M在以O为圆心,AD为直径的圆上,
连接OC交圆O于点![]() ,此时CM长度最短,
,此时CM长度最短,
在Rt△DOC中,CO=![]()
∴CM的最小值为![]() .
.
②2或8
如下图,过点C作CN⊥DE
由①可知∠DMA=90°
∵∠ADM+∠CDN=90°,∠ADM+∠DAM=90°
∴∠CDN=∠DAM
在△ADM和△CDN中
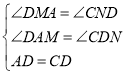
∴△ADM≌△CDN(AAS)
∴DN=AM
又∵CM=CD=4且CN⊥DE
∴DM=2DN=2AM,即![]()
∵∠DMA=90°
∴∠DAE=∠AMD,∠ADM=∠EDA
∴△DAE∽△DMA
∴![]()
∴t=AE=2
当点E到达点C,点F到达点D,此时AM=4,此时t=8
综上所述,当CM=4cm时,此时t的值为2或8.

【题目】一个二次函数图像上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … |
| 0 |
| 2 |
| 0 |
| -6 |
| … |
(1)![]() 的值为______;
的值为______;
(2)在给定的直角坐标系中,画出这个函数的图像;
(3)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.