题目内容
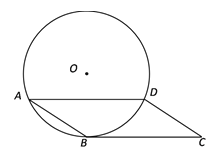
【题目】如图，在□ABCD中，AD是⊙O的弦，BC是⊙O的切线，切点为B．
（1）求证：
；
（2）若AB＝5，AD＝8，求⊙O的半径．
【答案】（1）证明见解析；（2）⊙O的半径为
【解析】
(1) 连接OB，根据题意求证OB⊥AD，利用垂径定理求证；
(2) 根据垂径定理和勾股定理求解.
解：（1）
连接OB,交AD于点E.
∵BC是⊙O的切线，切点为B，
∴OB⊥BC．
∴∠OBC＝90°
∵ 四边形ABCD是平行四边形
∴AD// BC
∴∠OED＝∠OBC =90°
∴ OE⊥AD
又 ∵ OE过圆心O
∴ 
（2）∵ OE⊥AD ,OE过圆心O
∴ AE=
AD=4
在Rt△ABE中，∠AEB＝90°，
BE＝
＝3，
设⊙O的半径为r，则OE=r－3
在Rt△ABE中，∠OEA＝90°，
OE2+AE2 = OA2
即(r－3)2+42= r2 ∴r=
∴⊙O的半径为
练习册系列答案
培优口算题卡系列答案
相关题目
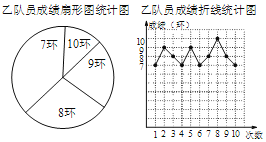
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛，特为甲、乙两名队员单行了一次选拔赛，要求这两名队员各射击10次，比赛结束后，根据比赛成绩情况，将甲，乙两名队员的比赛成绩制成了如下的统计图（表）：
甲队员的成绩统计表：
成绩（单位：环） | 7 | 8 | 9 | 10 |
次数（单位：次） | 5 | 1 | 3 | 1 |
（1）在乙队员成绩扇形统计图中，求“8环”所在扇形的圆心角的度数；
（2）经过整理，得到的分析数据如表：
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | 8 | b | 1 |
求表中的a、b、c的值（3）根据甲、乙两名队员的成绩情况，该射击队准备选派乙参加比赛，请你写出一条射击队选派乙的理由．
