题目内容
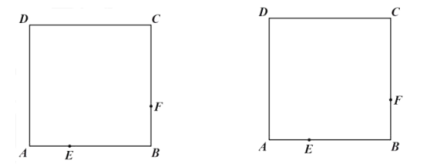
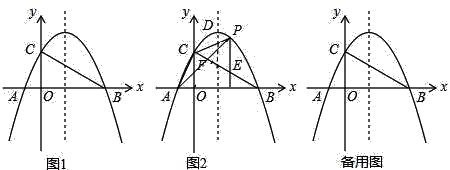
【题目】如图1,抛物线y=ax2+bx+c经过A(﹣2,0)、B(8,0)、C(0,4)三点,顶点为D,连结AC,BC.
(1)求抛物线的函数表达式及顶点D的坐标;
(2)判断三角形ABC的形状,并说明理由;
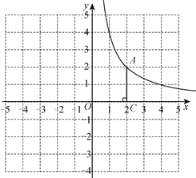
(3)如图2,点P是该抛物线在第一象限内上的一点.
①过点P作y轴的平行线交BC于点E,若CP=CE,求点P的坐标;
②连结AP交BC于点F,求![]() 的最大值.
的最大值.
【答案】(1)y=![]() x2+
x2+![]() x+4,顶点D坐标为(3,
x+4,顶点D坐标为(3,![]() );(2)三角形ABC是直角三角形,理由详见解析;(3)①P(4,6);②
);(2)三角形ABC是直角三角形,理由详见解析;(3)①P(4,6);②![]() .
.
【解析】
(1)设抛物线的解析式为y=a(x+2)(x-8),将点C的坐标代入可求得a的值,从而得到抛物线的解析式,然后依据抛物线的对称性得到抛物线的对称轴方程,将x=3代入可求得抛物线的顶点坐标.
(2)根据三角形ABC是直角三角形,求得AC2+BC2=AB2,即可利用勾股定理进行证明.
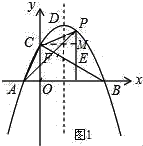
(3)①如图1所示:作CM⊥PE,垂足为M.先利用待定系数法求得BC的解析式,
设点P(m,﹣ ![]() m2+
m2+![]() m+4),则点E(m,﹣
m+4),则点E(m,﹣![]() m+4)﹐M(m,4),接下来依据等腰三角形的性质可得到PM=EM,从而得到关于m的方程,于是可求得点P的坐标.
m+4)﹐M(m,4),接下来依据等腰三角形的性质可得到PM=EM,从而得到关于m的方程,于是可求得点P的坐标.
②作PN⊥BC,垂足为N.先证明△PNE![]() △COB,由相似三角形的性质可知PN与PE的关系,然后再证明△PFN
△COB,由相似三角形的性质可知PN与PE的关系,然后再证明△PFN![]() △CAF,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得
△CAF,由相似三角形的性质可得到PF:AF与m的函数关系式,从而可求得![]() 最大值.
最大值.
(1)设抛物线的解析式为y=a(x+2)(x﹣8).
∵抛物线经过点C(0,4),
∴﹣16a=4,解得a=﹣![]() .
.
∴抛物线的解析式为y=﹣![]() (x+2)(x﹣8)=
(x+2)(x﹣8)=![]() x2+
x2+![]() x+4.
x+4.
∵A(﹣2,0)、B(8,0),
∴抛物线的对称轴为x=3.
∵将x=3代入得:y=![]() ,
,
∴抛物线的顶点D坐标为(3,![]() ).
).
(2)三角形ABC是直角三角形,理由如下:
∵AB=10,AC=2,BC=4![]() ,
,
∴AC2+BC2=AB2.
∴∠BCA=90°,所以三角形ABC是直角三角形.
(3) ①如图1所示:作CM⊥PE,垂足为M.
设直线BC的解析式为y=kx+b.
∵将B、C的坐标代入得:![]() ,解得k=﹣
,解得k=﹣![]() ,b=4,
,b=4,
∴直线BC的解析式为y=﹣![]() x+4.
x+4.
设点P(m,﹣ ![]() m2+
m2+![]() m+4),则点E(m,﹣
m+4),则点E(m,﹣![]() m+4),M(m,4).
m+4),M(m,4).
∵PC=EC,CM⊥PE,
∴PM=EM.
∴﹣![]() m2+
m2+![]() m+4﹣4=4﹣(﹣
m+4﹣4=4﹣(﹣![]() m+4),解得:m=0(舍去),m=4.
m+4),解得:m=0(舍去),m=4.
∴P(4,6).
②作PN⊥BC,垂足为N.

由①得:PE=﹣![]() m2+2m.
m2+2m.
∵PE∥y轴,PN⊥BC,
∴∠PNE=∠COB=90°,∠PEN=∠BCO.
∴△PNE∽△BOC.
∴![]() =
=![]() .
.
∴PN=![]() PE=
PE=![]() (﹣
(﹣![]() m2+2m).
m2+2m).
由(2)知∠BCA=90°,
又∵∠PFN=∠CFA,
∴△PFN∽△CAF.
∴ =﹣
=﹣![]() m2+
m2+![]() m.
m.
∴当m=4时,![]() 的最大值为
的最大值为![]() .
.