题目内容
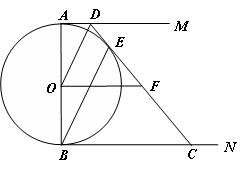
如图,AB是圆O的直径,AM和BN是圆O的两条切线,E是圆O上一点,D是AM上一点,连接DE并延长交BN于C,且OD∥BE,OF∥BN.
(1)求证:DE是圆O的切线;
(2)求证:OF=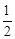 CD.
CD.

(1)求证:DE是圆O的切线;
(2)求证:OF=
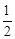 CD.
CD.见解析
证明:(1)连接OE,

∵AM是⊙O的切线,OA是⊙O的半径,
∴∠DAO=900。
∵OD∥BE,
∴∠AOD=∠OBE,∠DOE=∠OEB。
∵OB=OE,∴∠OEB=∠OBE。
∴∠AOD=∠DOE。
在△AOD和△DOE中,∵OA=OE,∠AOD=∠DOE,OD=OD,
∴△AOD≌△DOE(SAS)。∴∠DAO=∠DEO=900。
∴DE与⊙O相切。
(2)∵AM和BN是⊙O的两条切线,∴MA⊥AB,NB⊥AB。∴AD∥BC。
∵点O是AB的中点,OF∥BN,∴OF
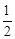 (AD+BC)。
(AD+BC)。
∵DE切⊙O于点E,∴DA=DE,CB=CE。
∴DC=AD+CB。∴OF=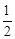 CD。
CD。
(1)连接OE,由已知,通过SAS证明△AOD≌△DOE,即可得∠DAO=∠DEO=900,从而得出结论。
(2)一方面由梯形中位线定理得到OF
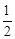 (AD+BC),另一方面由切线的性质,得DA=DE,CB=CE,从而证得结论。
(AD+BC),另一方面由切线的性质,得DA=DE,CB=CE,从而证得结论。

∵AM是⊙O的切线,OA是⊙O的半径,
∴∠DAO=900。
∵OD∥BE,
∴∠AOD=∠OBE,∠DOE=∠OEB。
∵OB=OE,∴∠OEB=∠OBE。
∴∠AOD=∠DOE。
在△AOD和△DOE中,∵OA=OE,∠AOD=∠DOE,OD=OD,
∴△AOD≌△DOE(SAS)。∴∠DAO=∠DEO=900。
∴DE与⊙O相切。
(2)∵AM和BN是⊙O的两条切线,∴MA⊥AB,NB⊥AB。∴AD∥BC。
∵点O是AB的中点,OF∥BN,∴OF

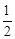 (AD+BC)。
(AD+BC)。∵DE切⊙O于点E,∴DA=DE,CB=CE。
∴DC=AD+CB。∴OF=
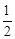 CD。
CD。(1)连接OE,由已知,通过SAS证明△AOD≌△DOE,即可得∠DAO=∠DEO=900,从而得出结论。
(2)一方面由梯形中位线定理得到OF

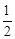 (AD+BC),另一方面由切线的性质,得DA=DE,CB=CE,从而证得结论。
(AD+BC),另一方面由切线的性质,得DA=DE,CB=CE,从而证得结论。
练习册系列答案
相关题目


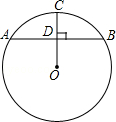

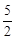 ,CD=4,则弦AC的长为 .
,CD=4,则弦AC的长为 .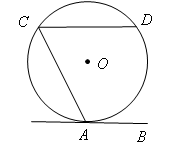
 的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是( ).
的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是( ).