题目内容
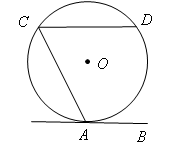
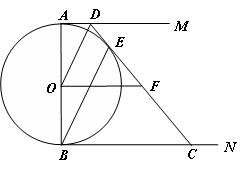
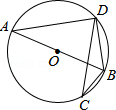
如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O 的半径为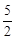 ,CD=4,则弦AC的长为 .
,CD=4,则弦AC的长为 .
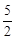 ,CD=4,则弦AC的长为 .
,CD=4,则弦AC的长为 .
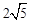 。
。连接OA,作OE⊥CD于E,则CE=DE=2,
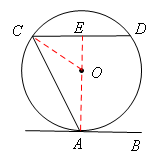
∵直线AB与⊙O相切于点A ,∴OA⊥AB。
∵CD∥AB,∴E、O、A三点共线。
连接OC,
在Rt△OEC中,OC=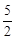 ,CE=2,由勾股定理得OE=
,CE=2,由勾股定理得OE=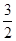 。∴AE=4。
。∴AE=4。
在Rt△AEC中,由勾股定理得AC=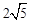 。
。

∵直线AB与⊙O相切于点A ,∴OA⊥AB。
∵CD∥AB,∴E、O、A三点共线。
连接OC,
在Rt△OEC中,OC=
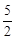 ,CE=2,由勾股定理得OE=
,CE=2,由勾股定理得OE=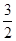 。∴AE=4。
。∴AE=4。在Rt△AEC中,由勾股定理得AC=
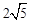 。
。
练习册系列答案
相关题目
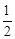 CD.
CD.
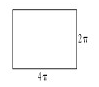

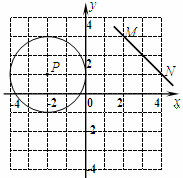
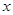 轴上截得的线段长度;
轴上截得的线段长度;