题目内容
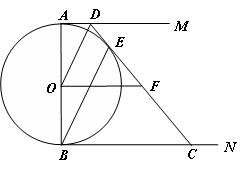
如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F.求证:直线EF是⊙O的切线.


见解析
证明:连接OE
∵AB=AC,∴∠ABC=∠C。
又∵OB=OE,∴∠ABC=∠OEB。
∴∠OEB=∠C。OE∥AC。
∵EF⊥AC,∴OE⊥EF。
∵OE是⊙O半径,∴直线EF是⊙O的切线。

连接OE,根据等腰三角形等边对等角的性质可得:∠ABC=∠C,∠ABC=∠OEB 从而∠OEB=∠C,根据同位角相等两直线平行的判定,得OE∥AC ,因此由EF⊥AC可得OE⊥EF,由切线的判定定理即可得出结论。
∵AB=AC,∴∠ABC=∠C。
又∵OB=OE,∴∠ABC=∠OEB。
∴∠OEB=∠C。OE∥AC。
∵EF⊥AC,∴OE⊥EF。
∵OE是⊙O半径,∴直线EF是⊙O的切线。

连接OE,根据等腰三角形等边对等角的性质可得:∠ABC=∠C,∠ABC=∠OEB 从而∠OEB=∠C,根据同位角相等两直线平行的判定,得OE∥AC ,因此由EF⊥AC可得OE⊥EF,由切线的判定定理即可得出结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
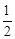 CD.
CD.




 B.28
B.28