题目内容
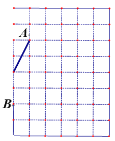
【题目】一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为____________海里/时.
【答案】![]()
【解析】
设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+40![]() =3x,解方程即可.
=3x,解方程即可.
如图所示:
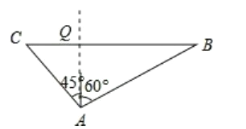
该船行驶的速度为x海里/时,
3小时后到达小岛的北偏西45°的C处,
由题意得:AB=80海里,BC=3x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°60°=30°,
∴AQ=![]() AB=40,BQ=
AB=40,BQ=![]() AQ=40
AQ=40![]() ,
,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=40,
∴BC=40+40![]() =3x,
=3x,
解得:x=![]() .
.
即该船行驶的速度为![]() 海里/时;
海里/时;
故答案为:![]() .
.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】为支援四川雅安地震灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
甲种货车 | 乙种货车 | |
载货量(吨/辆) | 45 | 30 |
租金(元/辆) | 400 | 300 |
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.