题目内容
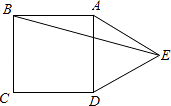
【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.
【答案】证明:连接AC,交BD于点O,作EG⊥BD于点G.
∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO= ![]() AC=
AC= ![]() BD=
BD= ![]() BE,
BE,
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
【解析】连接AC,交BD于点O,作EG⊥BD垂足为G,先证明四边形AOGE是矩形,从而可得到EG=![]() BD=
BD=![]() BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下
收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | 3 | ||
乙 | 6 | 3.2 |
分析数据、推断结论
(1)该校初二乙班共有40名同学,你估计读6本书的同学大概有_____人;
(2)你认为哪个班同学寒假读书情况更好,写出理由.