题目内容
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

【答案】(1)见解析(2)4.8
【解析】
(1)作∠A的角平分线交BC于D,则根据角平分线的性质可判断点D到边AB和边AC的距离相等;
(2)利用勾股定理计算出AD=6,设设点D到AB的距离为h,,利用等面积法得到![]() ×10h=8×6×
×10h=8×6×![]() ,然后解方程求出h即可.
,然后解方程求出h即可.
解:(1)作∠A的角平分线(或BC的垂直平分线)与BC的交点即为点D.
如图: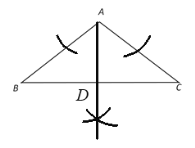
(2)∵AB=AC,AD是∠A角平分线
∴AD⊥BC,垂足为D,∵BC=16,
∴BD=CD=8,
∵AB=10,在RT△ABD中
∴根据勾股定理求得AD=6,
设点D到AB的距离为h,则![]() ×10h=8×6×
×10h=8×6×![]() ,解得h=4.8,
,解得h=4.8,
所以点D到边AB的距离为4.8.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目